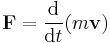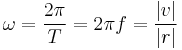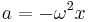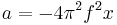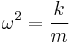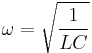Angular frequency

Not to be confused with angular velocity.
Classical mechanics
History of classical mechanics · Timeline of classical mechanics
Angular frequency is a measure of how fast an object is rotating

In physics, angular frequency ω (also referred to by the terms angular speed, radial frequency, circular frequency, orbital frequency, and radian frequency) is a scalar measure of rotation rate. Angular frequency (or angular speed) is the magnitude of the vector quantity angular velocity. The term angular frequency vector 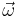\vec{\omega} is sometimes used as a synonym for the vector quantity angular velocity.[1]

In SI units, angular frequency is measured in radians per second, with units s−1 since radians are unitless.

One revolution is equal to 2π radians, hence[1][2]

\omega = {{2 \pi} \over T} = {2 \pi f} = \frac {|v|} {|r|}

where

ω is the angular frequency or angular speed (measured in radians per second),
T is the period (measured in seconds),
f is the ordinary frequency (measured in hertz),
v is the tangential velocity of a point about the axis of rotation (measured in meters per second),
r is the radius of rotation (measured in meters).

Angular frequency is therefore a simple multiple of ordinary frequency. However, using angular frequency is often preferable in many applications, as it avoids the excessive appearance of π. In fact, it is used in many fields of physics involving periodic phenomena, such as quantum mechanics and electrodynamics.

For example:

a = - \omega^2 x \;

Using 'ordinary' revolutions-per-second frequency, this equation would be:

a = - 4 \pi^2 f^2 x\;

Another often encountered expression when dealing with small oscillations or where damping is negligible is:[3]

\omega^{2} = \frac{k}{m}

where

k is the spring constant
m is the mass of the object.

This is referred to as the natural frequency.

Angular frequency inside an LC circuit can also be defined as the square root of the inverse of capacitance (measured in farads), times the inductance of the circuit (in henrys).[4]

\omega = \sqrt{1 \over LC}

See also

References and notes

  1. ↑ 1.0 1.1 Cummings, Karen; Halliday, David (Second Reprint: 2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley - India. pp. 449, 484, 485, 487. http://books.google.com/books?id=rAfF_X9cE0EC&printsec=copyright&rview=1&source=gbs_pub_info_s&cad=2. (UP1)
  2. ↑ Holzner, Steven (2006). Physics for Dummies. Hoboken, New Jersey: Wiley Publishing Inc. pp. 201. ISBN 978-0-7645-5433-9. http://books.google.com/books?id=FrRNO6t51DMC&pg=PA200&dq=angular+frequency&as_brr=3&rview=1. 
  3. ↑ Serway,, Raymond A.; Jewett, John W. (2006). Principles of physics - 4th Edition. Belmont, CA.: Brooks / Cole - Thomson Learning. pp. 375, 376, 385, 397. ISBN 9780534464790. http://books.google.com/books?id=1DZz341Pp50C&pg=PA376&dq=angular+frequency&rview=1. 
  4. ↑ Nahvi, Mahmood; Edminister, Joseph (2003). Schaum's outline of theory and problems of electric circuits. McGraw - Hill Companies (McGraw - Hill Professional). pp. 214, 216. ISBN 0071393072. http://books.google.com/books?id=nrxT9Qjguk8C&pg=PA103&dq=angular+frequency&lr=&rview=1. (LC1)

Related Reading: